Actividad: La rueda rueda
Recomendado para: 9 o 10 años
Nivel de Scratch: Inicial
Trabajo en aula: 2 horas
Una guía de MATCH: Aprendiendo Matemáticas con Scratch
Autores: Equipo de trabajo del Proyecto MATCH (FECYT-13-6677)
Resumen:
Navega al programa base en scratch.mit.edu
Vamos a hacer animaciones con ruedas. Para ello utilizaremos inicialmente un escenario con una línea del horizonte sobre la que rodará la rueda y estudiaremos despacio cómo hacer para simular el avance. Veremos que, si la rueda gira demasiado deprisa, parecerá que estamos derrapando. Por el contrario, si va demasiado despacio, el avance se verá poco realista. Para dar con la relación correcta entre avance y giro tendremos que calcular la longitud de la circunferencia. Con sólo esto, ya podremos animar un coche. Trabajando con varias ruedas de distintos tamaños, acabaremos animando tractores, bicicletas antiguas o cualquier otro vehículo con ruedas de distintos tamaños.
| Debemos saber | Aprenderemos |
|---|---|
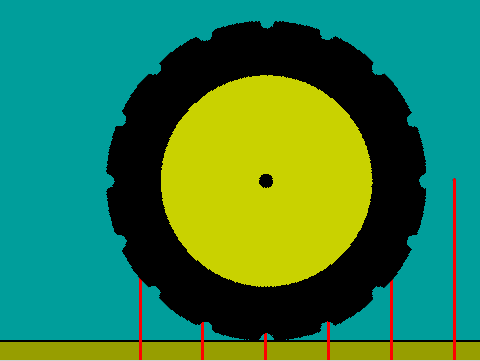
Figura 1: Apariencia del escenario en las primeras pruebas de rodaje
Incremento 1:
Proporcionamos a los alumnos el programa base que contiene el escenario con la línea del horizonte, la rueda de tractor y un lápiz. Como primera actividad, situaremos la rueda (moviéndola con el ratón) sobre la línea del horizonte y pulsaremos la tecla «L». Veremos cómo el lápiz traza una línea vertical desde el centro de la rueda hacia abajo (podremos borrar todos los trazos realizados pulsando la tecla «C». Dependiendo del tiempo del que se disponga, el lápiz se puede utilizar como base para la explicación de algunos comandos de pintado y apariencia de Scratch o, simplemente, como un objeto auxiliar del que únicamente nos preocupa su utilidad. Comenzaremos mostrando la pieza azul de giro en la rueda y veremos cómo, al poner ángulos pequeños, la rueda parece girar. Podemos dejar proyectado un «por siempre» y dejar unos minutos para que los alumnos prueben a hacer girar sus ruedas con diferentes velocidades.
Incremento 2:
Ahora vamos a mover la rueda al tiempo que gira. Si los alumnos ya conocen la pieza de «mover» en Scratch, es muy interesante dejarlos equivocarse y usarla en este contexto. Dado que la rueda está girando, el movimiento sucede en la dirección marcada según gira y la rueda comienza a trazar círculos. Esta exploración aclara muy bien la necesidad del uso de la pieza «cambiar x por», dado que queremos que nuestra rueda se mueva únicamente de derecha a izquierda. Introducida la mencionada instrucción, daremos unos minutos para que los alumnos prueben a hacer que la rueda gire y avance al tiempo.
Incremento 3:
Pediremos ahora que el movimiento de avance se produzca al pulsar la tecla de espacio (un avance por cada pulsación) como se muestra en la Figura 2. Dado que aún no hemos dicho nada sobre el radio, lo normal es que algunas ruedas derrapen y otras deslicen. Pediremos que intenten ajustar la relación entre uno y otro a ojo, intentando que su rueda muestre un comportamiento lo más real posible. Algunos alumnos intentarán ajustar el ángulo de giro y otros, el desplazamiento en el eje X. En cada paso pueden usar la tecla «L» para comprobar cuánto ha avanzado el centro de la rueda sobre la línea del horizonte.
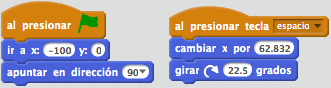
Figura 2: Código de la rueda a tamaño 100% (radio=160 unidades)
Incremento 4:
Cuando todos hayan comprendido la problemática, daremos el dato de que el radio son 160 unidades y, si no llegaran a establecer la conexión ellos, introduciremos la fórmula de la longitud de una circunferencia dado su radio. No se hará aquí mención a ninguna fórmula de la longitud del arco de una circunferencia, puesto que el objetivo es que establezcan la relación de proporcionalidad entre la longitud y el ángulo por sí mismos. Lo previsible es que la solución correcta aparezca en varias pantallas y se contagie por el aula. Debemos asegurarnos de que se entiende el código que se está copiando. Es también recomendable acordar giros que sean múltiplos o divisores de 22.5º para que las marcas de la rueda coincidan con la línea del horizonte antes de pasar al siguiente incremento.
Incremento 5:
Cambiamos ahora la apariencia de la rueda, usando la pieza de «fijar tamaño a ![]() %». Es más interesante el ejercicio si duplicamos el objeto rueda y tenemos varias ruedas con distintos tamaños. Al pulsar la tecla espaciadora debemos hacer que todas las ruedas que tenemos giren a la vez. Si se ha entendido el funcionamiento del lápiz, podemos asociarlo a la rueda que queramos en la pieza de «ir a», que sitúa el lápiz en el centro de la rueda que escojamos. También se puede duplicar el lápiz y cambiar los colores de los trazos para comprobar el avance de cada rueda.
%». Es más interesante el ejercicio si duplicamos el objeto rueda y tenemos varias ruedas con distintos tamaños. Al pulsar la tecla espaciadora debemos hacer que todas las ruedas que tenemos giren a la vez. Si se ha entendido el funcionamiento del lápiz, podemos asociarlo a la rueda que queramos en la pieza de «ir a», que sitúa el lápiz en el centro de la rueda que escojamos. También se puede duplicar el lápiz y cambiar los colores de los trazos para comprobar el avance de cada rueda.
Incremento 6:
Dibujamos un objeto nuevo que, con dos rectángulos, simule ser un coche. Con dos ruedas de igual tamaño, debemos conseguir que el coche se mueva de izquierda a derecha de la pantalla de manera solidaria a sus ruedas.
Incremento 7:
Aquellos alumnos que hayan resuelto con rapidez el incremento anterior, pueden plantearse hacer un tractor o una bicicleta antigua, con dos ruedas de diferente tamaño. El reto ahora es conseguir ajustar los ángulos de giro para que el avance horizontal sea el mismo y sin que ninguna de las dos ruedas derrape.
Explicación en vídeo
Créditos y patrocinadores
Editan: Y. Crespo, P. Espeso, M. Gonzalo, C. Hernández, B. Palop
Equipo de trabajo del Proyecto MATCH (FECYT-13-6677)
 |
||
 |
 |
 |
Volver a Match