Actividad: El cronómetro
Recomendado para: 9 o 10 años
Nivel de Scratch: Inicial
Trabajo en aula: 2 horas
Una guía de MATCH: Aprendiendo Matemáticas con Scratch
Autores: Equipo de trabajo del Proyecto MATCH (FECYT-13-6677)
Resumen:
Navega al programa base en scratch.mit.edu
Vamos a simular un cronómetro con números como los de un reloj digital. Para ello utilizaremos unos objetos cuyos disfraces representan cada cifra del cronómetro correspondientes a las unidades de los segundos, las decenas de los segundos, ídem para los minutos y las horas.
| Debemos saber | Aprenderemos |
|---|---|
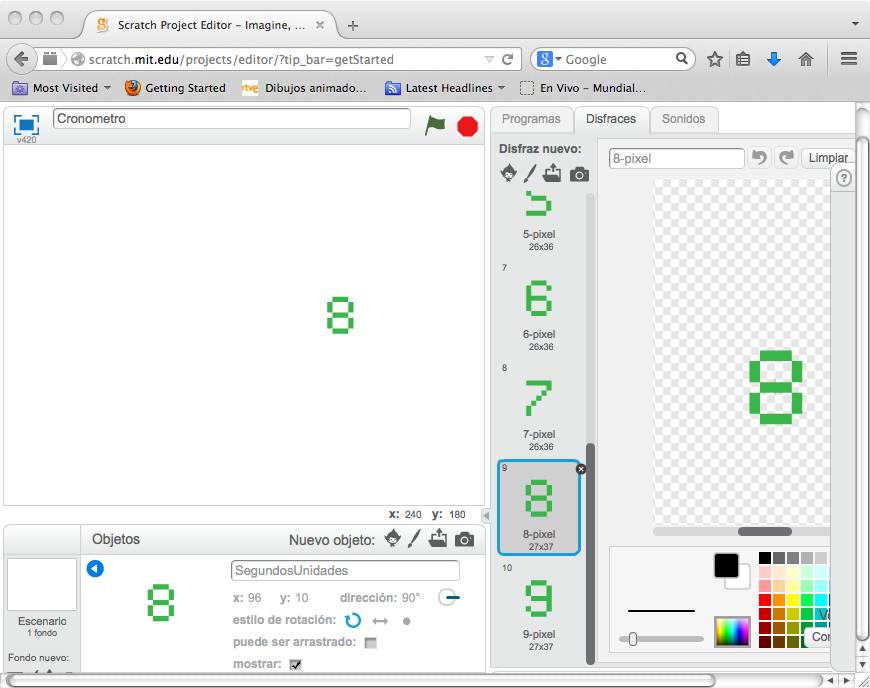
Figura 1: Crear un objeto a partir del archivo de letras
Incremento 1:
Los alumnos pueden poner el escenario base que deseen, les enseñaremos cómo obtener las cifras digitales de los objetos Scratch predefinidos. Deberán tener un objeto que llamaremos SegundosUnidades y que tendrá 10 disfraces, las cifras digitales del 0 al 9. Enseñamos cómo pasar al siguiente disfraz, consiguiendo pasar del 0 al 1, del 1 al 2, etc. y vuelta a empezar del 9 al 0.
Se recomienda explicar el código que se muestra en la Figura 2a. A continuación duplicamos el objeto, le llamamos SegundosDecenas y borramos el programa. En la Figura 2b se muestra el fragmento de código inicial de las decenas. Se ve cómo el objeto debe quedar posicionado igual en la vertical que las unidades de los segundos pero más a la izquierda.
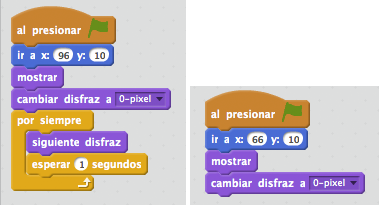
Figura 2: Códigos de apoyo para el incremento 1;
(2a, izda.) En las Unidades avanzamos sumando uno. Cuando sumamos 1, a la cifra digital 9 pasamos el 0;
(2b, dcha.) Preparamos las decenas para comenzar en 0 y en una posición igual en la vertical y a la izquierda en la horizontal
Es un buen momento para recordar cuestiones del sistema de coordenadas en el plano. La coordenada x representa la posición horizontal. Colocar el objeto más a la izquierda, más a la derecha, implica poner una x menor o mayor que la del objeto segundosUnidades. La coordenada y representa la posición vertical y debemos dejarla con el mismo valor que el objeto segundosUnidades. Invitamos a los alumnos a ver qué pasa al presionar bandera verde, cuando cambian las unidades del 9 al 0, deberá avanzar 1 las decenas, debemos pasar del 09 al 10 y de ahí al 11.
Incremento 2:
Vamos a contar los segundos que van pasando. Definimos una variable segundos. Al principio fijamos su valor a 0 y lo vamos aumentando en 1 cada vez que se avanza 1 segundo y se cambia de disfraz en las unidades. En la Figura 3. Comparamos cómo cambia del 09 al 10, del 19 al 20, del 29 al 30. Eso es lo que queremos. ¿Qué tienen en común los números en los que hay que cambiar? Es decir ¿qué tienen en común los cambios de decenas? Tenemos números divisibles entre 10, números que si los dividimos entre 10 el resultado es exacto. El resto de la división es 0. Esta es la forma que tenemos de saber si estamos ante un cambio en las decenas, la cantidad de segundos acumulada debe dar exacto al dividirlo entre 10, y esto significa que el resto de la división entre 10 es 0.
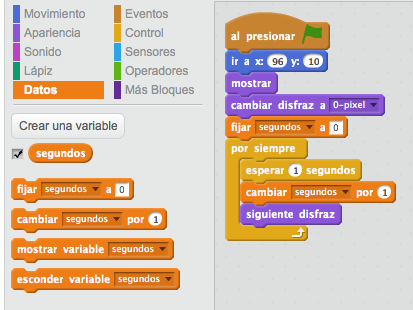
Figura 3: Contamos los segundos que han transcurrido
En la Figura 4 podemos ver los elementos necesarios para saber si la cantidad de segundos transcurridos en un momento dado es divisible entre 10. El operador n mod m realiza la división del número n entre el número m y obtiene como resultado el resto de la división entera. Ese valor preguntamos si es igual a 0 y si es el caso, entonces lanzamos un evento para que las decenas en los segundos se entere de que debe cambiar de disfraz.
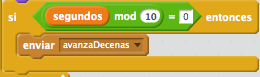
Figura 4: Elementos que tenemos que utilizar para saber si es 0 el resto de la división de los segundos transcurridos entre 10
Incremento 3:
Para ver el efecto rápido del cambio queremos acelerar el cronómetro y así no perder mucho tiempo para apreciar el resultado de lo que hemos hecho. Esto es habitual en simulación computarizada de procesos reales. Juguemos con la espera, pongamos a esperar 0.2 segundos.
Pero ¿qué observamos? Las decenas de segundos llegan a 60, 61, …, 99. Los segundos son 60 como máximo y en esto no se parecen a nuestro sistema métrico decimal. Por eso las cifras que pueden aparecer en las decenas de los segundos, no pueden llegar hasta el 9. Los alumnos deberán pensar qué disfraces borrar de los que contiene el objeto SegundosDecenas ¿Cuál será la cifra mayor?
Deberá comprobarse que del 59 se pasa al 00.
Incremento 4:
Si los alumnos han entendido el código para los segundos, y cómo las decenas cambian al llegar a múltiplos de 10, ahora queremos proponerles que hagan lo mismo poniendo 2 objetos nuevos que representarán los minutos. Necesitamos MinutosUnidades, MinutosDecenas. ¿Cuándo deberán cambiar las unidades de minutos? ¿De qué debe ser múltiplo la cantidad de segundos que vamos acumulando?
Se utilizará «enviar avanzaUnidadesMinutos».
Una vez que lo hemos conseguido, tendremos que ver cómo hacer para que cuando las unidades de minuto lleguen a 9 y pasen a 0, cambien las decenas de minutos. Los alumnos deberán pensar cada cuántos segundos sucede esto para poder enviar activar el evento «enviar avanzaDecenasMinutos».
Incremento 5:
Quizás 0.2 segundos de espera se hace largo para poder comprobar todo el cambio de los minutos. Vamos a jugar con la velocidad y el tiempo de espera. Definimos una variable velocidad. Igual que hicimos con la cantidad de segundos. La velocidad la fijamos al inicio en 1. Cambiaremos «esperar 0.2 segundos» por una expresión inversamente proporcional a la velocidad. De manera que cuando aumentemos el valor de la velocidad, el tiempo de espera disminuya.
Ayudados por el profesor los alumnos podrán llegar a la expresión 1/velocidad. Podemos jugar cambiando valores a velocidad y poniéndolos cada vez más grandes.
¿Qué pasa si quitamos la espera? Debe servirnos para reflexionar que hay un momento en que ya no puede aumentar más la velocidad porque hay una tarea que el ordenador hace («cambiar de disfraz») que ocupa un tiempo en hacerla.
Por último se puede poner la variable como un slider en la pantalla para que el alumno pueda jugar a aumentar su valor y a disminuirlo.
Nótese que la variable empieza en valor 1. ¿Qué pasará cuando un alumno le disminuya el valor y le ponga 0?
Incremento 6:
¿Querrían algunos pensar qué hacer si también añadimos las horas a nuestro cronómetro?
El alumno que esté motivado y haya conseguido avanzar podrá mejorar el proyecto de varias formas. Si se detiene el programa no vuelve a cero pero si se presiona la tecla r vuelve todo a cero.
También es posible comprobar si el número representado con los disfraces de números digitales corresponde al valor de la variable segundos.
El proyecto que contiene todos los incrementos realizados se puede consultar aquí
Explicación en vídeo
Créditos y patrocinadores
Editan: Y. Crespo, P. Espeso, M. Gonzalo, C. Hernández, B. Palop
Equipo de trabajo del Proyecto MATCH (FECYT-13-6677)
 |
||
 |
 |
 |
Volver a Match